count number of rectangles containing each point

leetcodecoding-test이진탐색binary-search

문제 원문

[! info] 문제 링크 https://leetcode.com/problems/count-number-of-rectangles-containing-each-point/

You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).

The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).

Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jthpoint.

The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.

Example1:

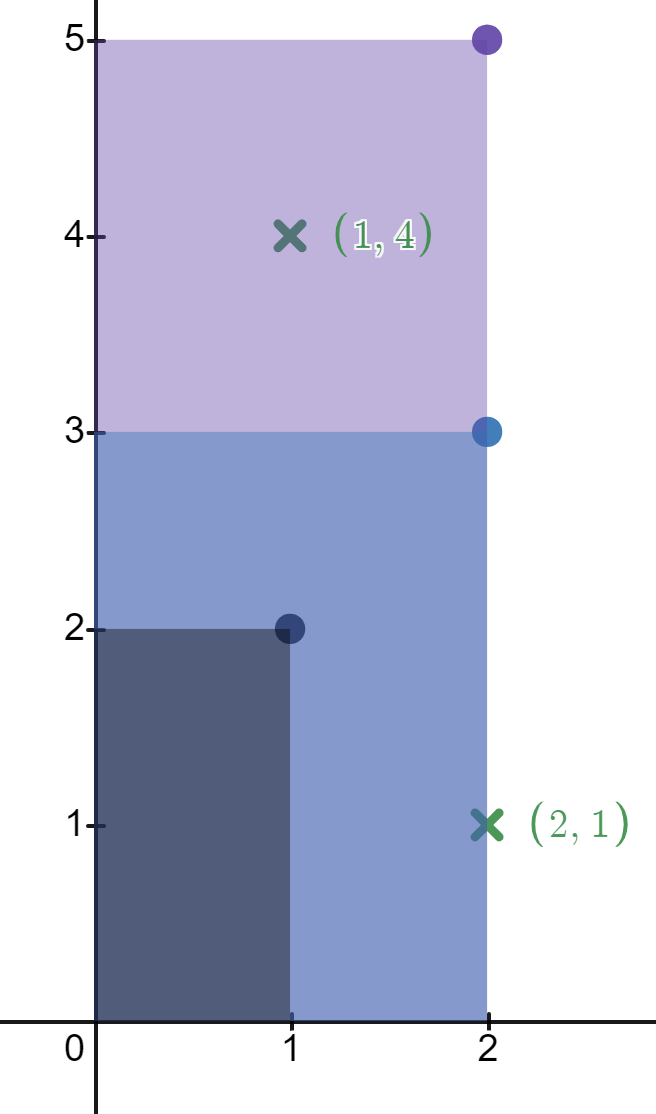
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]] Output: [2,1] Explanation: The first rectangle contains no points. The second rectangle contains only the point (2, 1). The third rectangle contains the points (2, 1) and (1, 4). The number of rectangles that contain the point (2, 1) is 2. The number of rectangles that contain the point (1, 4) is 1. Therefore, we return [2, 1].

Example 2:

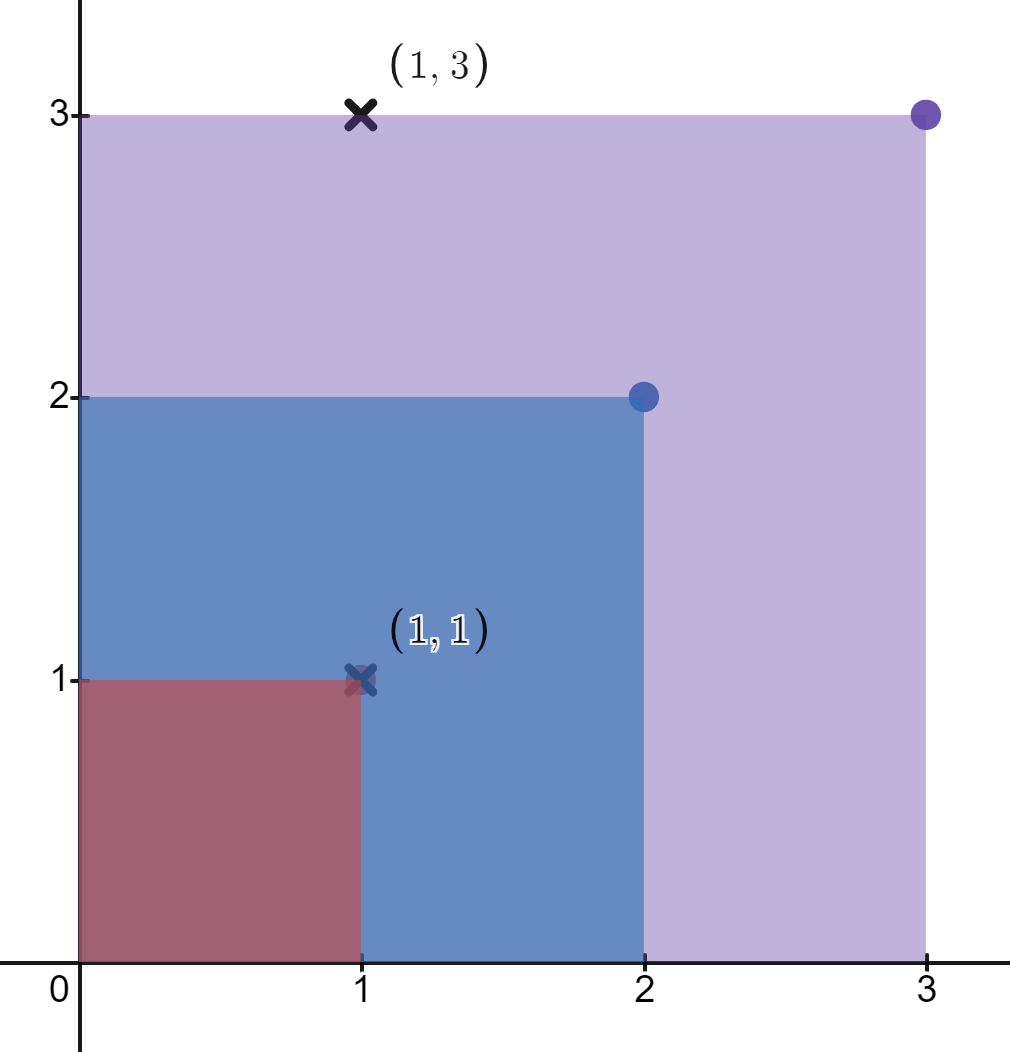
Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]] Output: [1,3] Explanation: The first rectangle contains only the point (1, 1). The second rectangle contains only the point (1, 1). The third rectangle contains the points (1, 3) and (1, 1). The number of rectangles that contain the point (1, 3) is 1. The number of rectangles that contain the point (1, 1) is 3. Therefore, we return [1, 3].

Constraints:

• 1 <= rectangles.length, points.length <= 5 * 104
• rectangles[i].length == points[j].length == 2
• 1 <= li, xj <= 109
• 1 <= hi, yj <= 100
• All the rectangles are unique.
• All the points are unique.

문제 설명

[! abstract]

모든 사각형의 시작은 (0,0) 에서 시작한다.

rectangles = [(x,y),(x,y)...] ⇒ 여러 사각형들의 우측 상단 꼭짓점의 좌표가 들어있다. points=[(x,y),(x,y)...]⇒ 임의의 꼭짓점들이 들어있다.

각 points 안의 임의의 점 마다. rectangles 안의 몇개의 사각형 안에 포함되는지 계산한 리스트를 리턴해야 한다.

제한 사항

• $1<=사각형의갯수,비교해야하는꼭짓점의갯수<=5\ast 10^4$
• $사각형의꼭짓점좌표==비교해야하는꼭짓점의좌표==2$ (x,y) 2개
• $1<=사각형의x좌표,비교해야하는꼭짓점의x좌표<=10^9$
• $1<=사각형의y조표,비교해야하는꼭짓점의y좌표<=100$
• All the rectangles are unique.
• All the points are unique.

풀이

첫번째 접근

brute-force 를 활용하여 단순하게 접근하면 풀수 있을것으로 생각된다.

class Solution:
    def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:
	    # 결과값을 담을 리스트를 만들고
        res=[0 for _ in range(len(points))] #
		# while 문을 통해 사각형들을 하나씩 빼내어 결과와 맞는 꼭짓점을 계산해 하나씩 더해주었다.
        while rectangles:
            x,y=rectangles.pop()
            for i in range(len(points)):
                p_x,p_y=points[i]
                if x>=p_x and y>=p_y:
                    res[i]+=1
        return res

[! fail] 시간 제약에 막혀 성공하지 못하였다.

Question

첫번째 접근에서의 문제점을 확인하고 고쳐야 한다. 어떤 부분을 고칠수 있을까?

첫번째 접근의 실패 이유

시간 제약을 해결할 수 있는 방안을 찾아보기 위해 스스로 질문해보자.

1. 중복되는 계산이 있는가?
   1. 순서대로 하나씩 확인하여야 하기 때문에 순차적으로 진행하면서 중복되는 계산이 있지는 않다.
   2. 모든 사각형과 꼭짓점이 유일한 좌표이기 때문에 메모리를 사용하여 중복계산을 줄일곳이 없다.
2. 불필요한 동작을 수행하는 코드가 있는가?
   1. 순차적으로 존재하는 리스트를 pop 해가며 계산을 진행하였기 때문에 모든 경우를 비교한다는 생각에 한해서는 불필요한 동작을 하는 코드가 있어보이지 않는다.

코드만 개선해서는 불필요한 시간을 줄일수 없다고 판단하여 다른 방식을 생각해야할것으로 보인다.

해결 방안

데이터를 정재하여 접근과 찾는 시간을 줄여야 한다.

두번째 접근

제약 사항을 확인해 봤을 때 좌표의 y 값은 최고 가 100 으로 상대적으로 굉장히 낮은 값인걸 확인했다.

따라서 데이터를 y값에 해당하는 x좌표의 리스트를 할당하여 딕셔너리 형태의 데이터로 정재하여 원하는 데이터에 대한 접근을 쉽게 하고자 하였다.

키값에 할당된 x 리스트가 정렬되어 있는 상황이라면 points 의 좌표 p_x 가 x 리스트의 몇번째 인덱스보다 크고 작은지 확인하고 해당 인덱스까지의 갯수를 찾는다면 쉽게 포함하는 위치를 찾을 수 있다.

from bisect import bisect_left
class Solution:
    def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:
	    res=[]
	    # 먼저 y 값을 키값으로 갖는 딕셔너리를 만든다.
	    arranged={y:[] for x,y in rectangles}
	    # y값에 해당하는 x 좌표들을 리스트에 넣어준다.
	    for x,y in rectangles:
		    arranged[y].append(x)
		# 리스트들을 정렬한다.
		for i in arranged:
			arranged[i].sort()
			
		for p_x,p_y in points:
			count=0
			for y in arranged:
				# 만약 사각형의 y 좌표가 p_y 와 같거나 크다면 조건에 부합할 가능성이 있다.
				if y>=p_y:
					# 조건에 부합할 수 있는 y에 해당하는 x 리스트
					list_x=arranged[y]
					# x 리스트 안의 요소들도 y 와 같은 원리로 찾을 수 있다.
					# 만약 선형 탐색을 활용하여 탐색한다면 brute force 와 다를게 없기 때문에 
					# 시간초과가 날 것이다.
					# 찾는 요소에 대한 정확한 정보가 없기 때문에 이진 탐색을 진행해야 한다.
					count+=len(list_x)-bisect_left(list_x,p_x)
			res.append(count)
        return res

[! tip] 해결을 위한 조건 이진탐색(binary-search)을 활용하여 조건에 맞는 탐색의 시간을 줄여야 한다.